BLS Signatures: A Technical Deep Dive into Implementation and Curves

Introduction

BLS (Boneh-Lynn-Shacham) signatures represent a sophisticated cryptographic scheme that leverages pairing-friendly elliptic curves to enable unique features like signature aggregation and threshold signing. Let's explore the technical intricacies of BLS signatures, focusing on implementation details, supported curves, and their mathematical foundations.

Mathematical Foundation

Bilinear Pairings

BLS signatures are built on bilinear pairings, specifically Type-3 pairings, which are maps e: G1 × G2 → GT, where:

• G1 and G2 are additive groups of prime order r
• GT is a multiplicative group of the same order
• The pairing is bilinear: e(aP, bQ) = e(P,Q)^(ab)

Core Operations

1. Key Generation:

# Private key is a random scalar
sk ← random(Fr)
# Public key is a point in G1
pk = sk * G1_generator

2. Signing:

# Message is hashed to a point in G1
H = hash_to_curve(message)
# Signature is in G2
signature = sk * H

3. Verification:

# Check if pairing equation holds
e(pk, H) == e(G1_generator, signature)

Supported Curves and Their Properties

BLS12-381

Currently the most widely adopted curve for BLS signatures, offering:

• 128-bit security level
• Optimized for signature aggregation
• Parameters:
  • p = 0x1a0111ea397fe69a4b1ba7b6434bacd764774b84f38512bf6730d2a0f6b0f6241eabfffeb153ffffb9feffffffffaaab
  • r = 0x73eda753299d7d483339d80809a1d80553bda402fffe5bfeffffffff00000001

BN254 (alt_bn128)

Used in earlier implementations:

• 100-bit security level (no longer recommended for high-security applications)
• Faster computations compared to BLS12-381
• Smaller parameter sizes

Why These Curves?

The selection of curves is based on several critical factors:

1. Security Requirements:

   • Must resist known attacks (MOV, STNFS)
   • Embedding degree k=12 for efficient pairing computation
   • Prime order groups

2. Performance Considerations:

   • Efficient endomorphisms available
   • Tower field arithmetic optimization
   • Low hamming weight parameters

3. Implementation Properties:

Technical Implementation Details

Signature Aggregation

# Aggregate n signatures
def aggregate_signatures(sigs):
    return sum(sigs) # Point addition in G2
 
# Verify aggregate signature
def verify_aggregate(pubkeys, messages, aggregate_sig):
    return e(sum([pk_i * hash_to_curve(msg_i) for pk_i, msg_i in zip(pubkeys, messages)], 
             G2_generator) == e(G1_generator, aggregate_sig)

Optimization Techniques

1. Batch Verification:

2. Subgroup Checks:

• Essential for security
• Can be optimized using endomorphisms
• Different strategies for G1 and G2

Real-World Applications and Performance

Ethereum 2.0 Implementation

• Uses BLS12-381 for validator signatures
• Aggregates up to 128 signatures per block
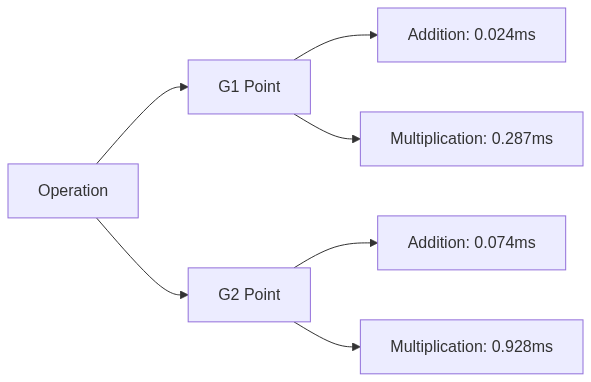
• Verification cost breakdown:
  • G1 operations: ~0.6ms
  • G2 operations: ~1.2ms
  • Pairing: ~7ms

Performance Metrics

Security Considerations

1. Implementation Requirements:

   • Constant-time operations
   • Secure random number generation
   • Proper subgroup checking
   • Protection against rogue key attacks

2. Known Attack Vectors:

   • Small subgroup attacks
   • Invalid curve attacks
   • Rogue key attacks in aggregation

Future Developments

1. Post-Quantum Considerations:

   • Research into quantum-resistant pairing-based signatures
   • Hybrid schemes exploration

2. Performance Optimizations:

   • New curve proposals
   • Implementation improvements
   • Hardware acceleration

This technical deep dive into BLS signatures demonstrates the complexity and elegance of modern cryptographic systems. The careful selection of curves and implementation details is crucial for both security and performance in real-world applications.